
Codeforces Round 965 (Div. 2)
锐评
A,B都是构造,像是构造专场
能上分真开心,最后C题差一点没搞出来,外界大脑得以拿下
A. Find K Distinct Points with Fixed Center
题目大意
我想不出一个好的标题,所以决定向 LeetCode 学习。
- 孙子兵法
给你三个整数 x_c 、 y_c 和 k ( -100 \leq x_c, y_c \leq 100 , 1 \leq k \leq 1000 )。
您需要找到 k 个分点( -100 \leq x_c, y_c \leq 100 , 1 \leq k \leq 1000 )。**点( x_1, y_1 ),( x_2, y_2 ), \ldots ,( x_k, y_k ),在二维坐标平面上具有整数坐标,使得:
- 它们的中心 ^{\text{∗}} 是( x_c, y_c )。
- 从 1 到 k 的所有 i 的 -10^9 \leq x_i, y_i \leq 10^9 。
可以证明,至少有一组 k 不同的点总是满足这些条件的。
^{\text{∗}} k 点( x_1, y_1 ),( x_2, y_2 ), \ldots ,( x_k, y_k )的圆心是 \left( \frac{x_1 + x_2 + \ldots + x_k}{k}, \frac{y_1 + y_2 + \ldots + y_k}{k} \right) 。
输入描述
第一行包含 t ( 1 \leq t \leq 100 ) - 测试用例数。( 1 \leq t \leq 100 ) - 测试用例的数量。
每个测试用例包含三个整数 x_c 、 y_c 和 k ( -100 \leq x_c, y_c \leq 100 , 1 \leq k \leq 1000 )--中心坐标和必须输出的不同点的数量。
保证所有测试用例中 k 的总和不超过 1000 。
输出描述
第一行包含 t ( 1 \leq t \leq 100 ) - 测试用例数。( 1 \leq t \leq 100 ) - 测试用例的数量。
每个测试用例包含三个整数 x_c 、 y_c 和 k ( -100 \leq x_c, y_c \leq 100 , 1 \leq k \leq 1000 )--中心坐标和必须输出的不同点的数量。
保证所有测试用例中 k 的总和不超过 1000 。
样例输入
4
10 10 1
0 0 3
-5 -8 8
4 -5 3
样例输出
10 10
-1 -1
5 -1
-4 2
-6 -7
-5 -7
-4 -7
-4 -8
-4 -9
-5 -9
-6 -9
-6 -8
1000 -1000
-996 995
8 -10
思路
签到其实没什么好说的,只要着重看最后一个条件,也就是x和y向左移动多少就要向右移动多少,并且必须配对,如果是奇数就加一个x和y本身就好。所以构造出来就是x - 1,y - 1;x + 1,y + 1,x - 2,y - 2;x + 2,y + 2···
实现方法有很多,随便写一个。
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int N = 1e6 + 9;
const int MOD = 998244353;
int x, y, k;
void solve() {
cin >> x >> y >> k;
int cnt = 1;
if (k % 2 == 1) {
cout << x << " " << y << "\n";
k --;
}
if (k) {
for (int i = 1; i <= k; ++ i) {
cout << x - cnt << " " << y - cnt << "\n";
if (i & 1) cnt = - cnt;
else {
cnt = - cnt;
cnt ++;
}
}
}
}
signed main() {
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
int _ = 1;
cin >> _;
while (_--) {
solve();
}
return 0;
}
B. Minimize Equal Sum Subarrays
题目大意
众所周知,农夫约翰喜欢排列组合,但我也喜欢!
- 孙子,《排列组合的艺术
给你一个长度为 n 的排列组合 * 。长度为 n 的排列组合 p 。
求一个长度为 n 的排列组合 q 使 pi + p{i+1} + ... + pj = qi + q{i+1} + ... + qj 的成对数 (i, j) ( 1 ≤ i ≤ j ≤ n ) 最小。
- 长度为 n 的排列是由 1 至 n 的 n 个不同整数按任意顺序排列而成的数组。例如, [2,3,1,5,4] 是一个排列,但 [1,2,2] 不是一个排列(2 在数组中出现了两次), [1,3,4] 也不是一个排列(n=3 但数组中有 4)。
输入描述
第一行包含 t ( 1 \leq t \leq 10^4 ) - 测试用例数。
每个测试用例的第一行包含 n ( 1 \leq n \leq 2 \cdot 10^5 )。
下一行包含 n 个空格分隔的整数 p_1, p_2, \ldots, p_n ( 1 \leq p_i \leq n ) - 表示长度为 n 的排列 p 。
保证所有测试用例中 n 的总和不超过 2 \cdot 10^5 。
输出描述
针对每个测试用例,输出一行包含长度为 n 的任意排列组合(排列组合q),使得q的配对数最小。
样例输入
3
2
1 2
5
1 2 3 4 5
7
4 7 5 1 2 6 3
样例输出
2 1
3 5 4 2 1
6 2 1 4 7 3 5
思路
用两个前缀和只差相等的对数最少,猜了很多结论,最后发现我答案的某一片区域再给出排列的对应区域的右侧即可
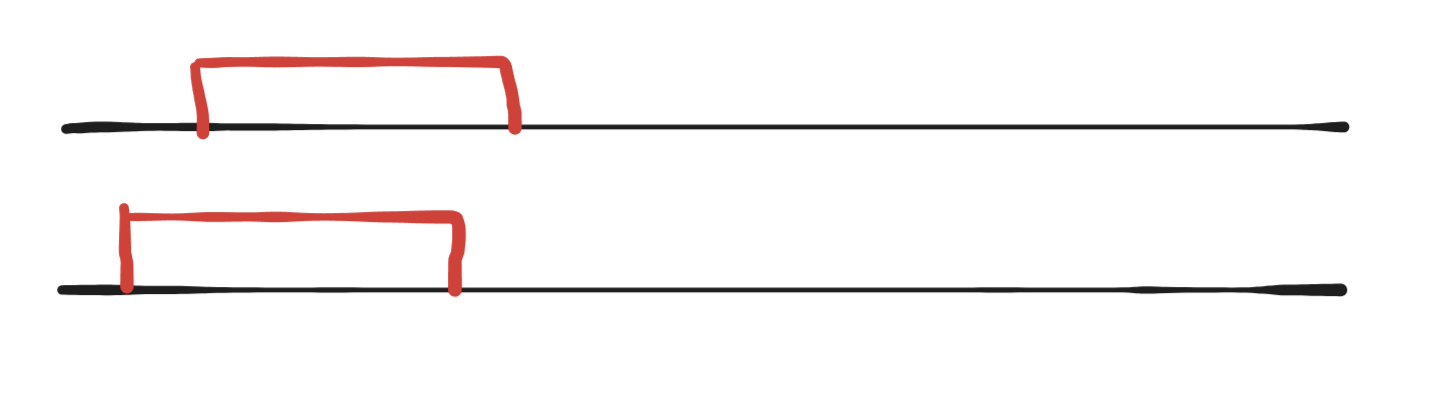
像是这样总是红色的相对应,而原排列右侧突出部分不可能和左侧缺少部分相等,因此依次向右移动即可,如果不理解直接看代码,再模拟一下样例就可以了,最终应该都是相等的对数为0。
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int N = 1e6 + 9;
const int MOD = 998244353;
int n, m;
int a[N], pre[N];
void solve() {
cin >> n;
pre[0] = 0;
for (int i = 1; i <= n; ++ i)
cin >> a[i], pre[i] = pre[i - 1] + a[i];
for (int i = 1; i < n; ++ i) {
cout << a[i + 1] << " ";
}
cout << a[1] << "\n";
}
signed main() {
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
int _ = 1;
cin >> _;
while (_--) {
solve();
}
return 0;
}
C. Perform Operations to Maximize Score
题目大意
我看到萨蒂亚姆343了。我在发抖这次请多出一些中值问题。我喜欢这些求求你,satyam343,我们相信你。
- satyam343最忠实的粉丝
给你一个长度为 n 的数组 a 和一个整数 k 。同时给你一个长度为 n 的二进制数组 b 。
您最多可以执行以下操作 k 次:
- 选择一个索引 i ( 1 \leq i \leq n ),使得 b_i = 1 .设置 a_i = a_i + 1 (即在 a_i 的基础上增加 1 )。
您的得分定义为 \max\limits_{i = 1}^{n} \left( a_i + \operatorname{median}(c_i) \right) ,其中 c_i 表示从 a 中删除 a_i 后得到的长度为 n-1 的数组。换句话说,您的得分是 1 至 n 的所有 i 中 a_i + \operatorname{median}(c_i) 的最大值。
请找出如果以最佳方式进行运算,您能得到的最高分。
对于任意数组 p , \operatorname{median}(p) 被定义为 p 的 \left\lfloor \frac{|p|+1}{2} \right\rfloor -th 最小元素。例如, \operatorname{median} \left( [3,2,1,3] \right) = 2 和 \operatorname{median} \left( [6,2,4,5,1] \right) = 4 。
输入描述
第一行包含一个整数 t ( 1 \leq t \leq 10^4 ) - 测试用例的数量。
每个测试用例以两个整数 n 和 k ( 2 \leq n \leq 2 \cdot 10^5, 0 \leq k \leq 10^9 ) 开头 — a 的长度和可以执行的操作数。
下面一行包含 n 个空格分隔的整数 a_1, a_2, \ldots, a_n ( 1 \leq a_i \leq 10^9 ) - 表示数组 a 。
下面一行包含 n 个空格分隔的整数 b_1, b_2, \ldots, b_n ( b_i 是 0 或 1 ),表示数组 b 。
保证所有测试用例中 n 的总和不超过 2 \cdot 10^5 。
输出描述
对于每个测试用例,在新行中输出所能得到的最大分值。
样例输入
8
2 10
3 3
1 1
3 10
3 3 3
0 0 0
4 4
2 1 5 1
0 1 0 1
5 4
7 5 2 5 4
0 0 1 0 1
5 1
5 15 15 2 11
1 0 0 1 1
5 2
10 11 4 10 15
1 1 0 1 0
4 4
1 1 2 5
1 1 0 0
2 1000000000
1000000000 1000000000
1 1
样例输出
16
6
8
13
21
26
8
3000000000
思路
外接大脑的一集
如果最大值a可以加的话,那么加最大值一定是最优解
否则二分答案二分出中值最大是几,在特判能不能将一些可以改变的a值加到最大比原来那最大值更大,以上所有操作都取Max即可
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int N = 1e6 + 9;
const int MOD = 998244353;
#define int long long
int n, m, k;
pair<int,int> a[N];
bool check(int mid, pair<int,int> a[]) {
if (a[n / 2].first >= mid) return true;
int cnt = 0;
for (int i = 1; i <= n - 1; ++ i) {
if (a[i].first >= mid) cnt ++;
}
int chuang = 0;
chuang = (n - 1) / 2 + 1 - cnt;
int xuqiu = 0, cntt = 0;
vector<int> vue;
for (int i = 1; i <= n - 1; ++ i) {
if (a[i].second == 1 && a[i].first < mid) {
vue.push_back(a[i].first);
}
}
if (vue.size() < chuang) return false;
reverse(vue.begin(),vue.end());
for (int i = 0; i < chuang; ++ i) {
xuqiu += (mid - vue[i]);
}
return xuqiu <= k;
}
void solve() {
cin >> n >> k;
int t = n / 2;
for (int i = 1; i <= n; ++ i) cin >> a[i].first;
for (int i = 1; i <= n; ++ i) cin >> a[i].second;
sort(a + 1, a + 1 + n);
int res = a[n].first;
if (a[n].second == 1) {
res = max(res, a[n].first + k + a[t].first);
}else {
int l = 1, r = 1e10;
while (l < r) {
int mid = l + r + 1 >> 1;
if (check(mid, a)) l = mid;
else r = mid - 1;
}
res += l;
int idx = 0;
for (int i = n; i >= 1; -- i) {
if (a[i].second == 1) {
idx = i;
break;
}
}
if (idx != 0) {
if (a[idx].first + k >= a[n].first) {
int res1 = a[idx].first + k;
int b[n + 1];
int j = 1;
for (int i = 1; i <= n; ++ i) {
if (i == idx) continue;
b[j ++] = a[i].first;
}
res1 += b[j / 2];
res = max(res, res1);
}
}
}
cout << res << "\n";
}
signed main() {
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
int _ = 1;
cin >> _;
while (_--) {
solve();
}
return 0;
}

