数论基础 | 第九洒月光

数论基础之——整除

两数相除余数为0则为整除

\text { 设 } a, b \in \mathbf{Z} ， a \ne 0 \text { 。如果 } \exists q \in \mathbf{Z} \text { ，使得 } b=a q \text { ，那么就说 } b \text { 可被 } a \text { 整除，记作 } a \mid b \text {; }

整除性质

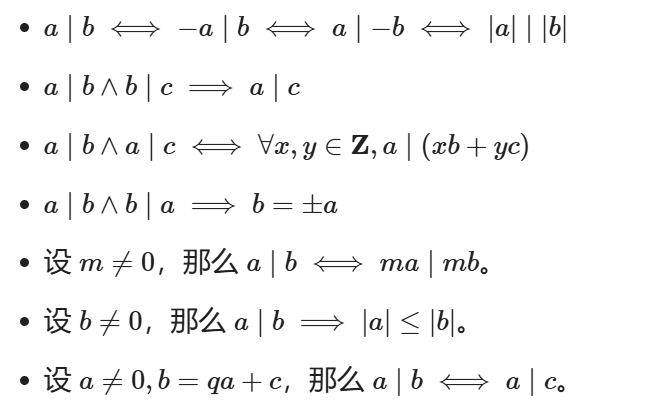
数论基础之——约数

tips:default 定义：若 a 能整除 b ，则称 b 是 a 的倍数，a 是 b 的约数。

tips:default 性质：设整数 b （b不为0），当一个数 d 遍历 b 的全部约数时，b / d 也遍历 b 的全体约数设整数 b > 0，则当 d 遍历 b 的全体正约束的时候，b / d 也遍历 b 的全部正约数

最大公因数

定义：

多个数共有的因数称为公因数，其中最大的为最大公因数。记作（a, b）

性质：

最大公因数的求法

欧几里得算法

// Version 1
int gcd(int a, int b) {
  if (b == 0) return a;
  return gcd(b, a % b);
}

// Version 2
int gcd(int a, int b) { return b == 0 ? a : gcd(b, a % b); }

递归至 b = 0（即上一步的 a % b = 0）的情况再返回值即可。

根据上述递归求法，我们也可以写出一个迭代求法：

int gcd(int a, int b) {
  while (b != 0) {
    int tmp = a;
    a = b;
    b = tmp % b;
  }
  return a;
}

另外，对于 C++17，我们可以使用头中的 std::gcd 与 std::lcm 来求最大公约数和最小公倍数。

多个数的最大公因数

那怎么求多个数的最大公约数呢？显然答案一定是每个数的约数，那么也一定是每相邻两个数的约数。我们采用归纳法，可以证明，每次取出两个数求出答案后再放回去，不会对所需要的答案造成影响。

最小公倍数

定义：多个数共有的倍数称为公倍数，其中最小的为最小公倍数。记作[a, b]。

一组整数的公倍数，是指同时是这组数中每一个数的倍数的数。0 是任意一组整数的公倍数。

一组整数的最小公倍数，是指所有正的公倍数里面，最小的一个数。

最小公倍数求法

int lcm(int a,int b)
{
    return (a / gcd(a, b)) * b;//防止数据溢出
}

素数与合数

定义：

性质：

算数基本引理

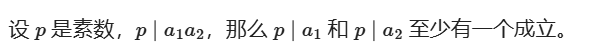
唯一分解定理

C/C++的整数除法和取模运算

在 C/C++ 中，整数除法和取模运算，与数学上习惯的取模和除法不一致。

对于所有标准版本的 C/C++，规定在整数除法中：

当除数为 0 时，行为未定义；
否则 (a / b) * b + a % b 的运算结果与 a 相等。

也就是说，取模运算的符号取决于除法如何取整；而除法如何取整，这是实现定义的（由编译器决定）。

从 C99和 C++11标准版本起，规定 商向零取整（舍弃小数部分）；取模的符号即与被除数相同。从此以下运算结果保证为真：

5 % 3 == 2;
5 % -3 == 2;
-5 % 3 == -2;
-5 % -3 == -2;