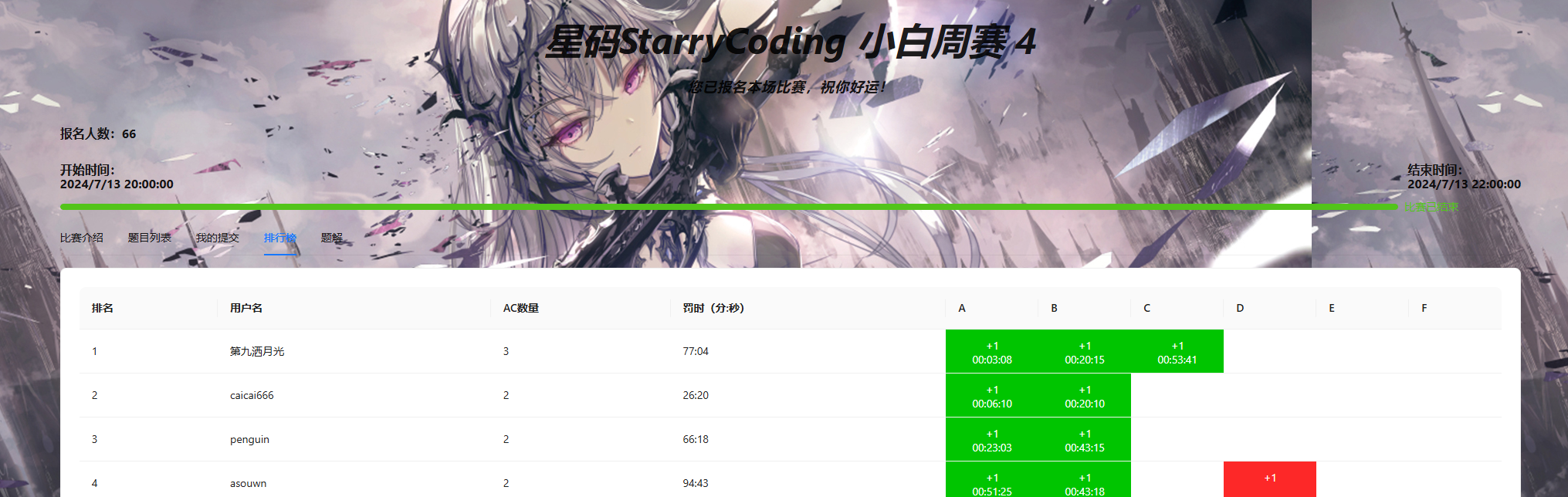
星码StarryCoding 小白周赛 4
锐评一下
感觉题目还是有难度的,最终止步于C题,但是是第一哈哈哈哈哈(bushi),后面看到E题其实思路蛮简单,但是不会实现,基础还是差一些,
A. 花园浇水
题目描述
小杨想要给花园浇水,花园总长度为𝑘,小杨有𝑛个水桶,其中第𝑖个水桶可以让他每小时浇灌长度为𝑎𝑖,且水桶中的水是无限的。
小杨不能给已经浇过水的部分浇水,也不能浇到地面上。
小杨只能选择一个水桶,请帮助他确认浇灌整个花园所需的最少小时数。
输入格式
第一行输入包含两个整数 𝑛 , 𝑘(1 ≤ 𝑛, 𝑘 ≤ 100),分别表示水桶的个数和花园的长度。
第二行输入包含𝑛n个整数 𝑎𝑖 (1 ≤ 𝑎𝑖 ≤ 100),𝑎𝑖表示第𝑖个水桶每小时可浇灌的区域长度。
输出格式
若可以在整数小时内浇灌整个花园,则输出浇灌花园所需的最少小时数;
否则输出-1。
输入样例1
3 6
2 3 5输出样例1
2输入样例2
3 6
4 5 7输出样例2
-1思路
其实A肯定是签到题,这个题也不可能会很难,不能把水浇地上也不能重复浇,其实就意味着总共的长度和浇水的速度要成正比,这样才能保住最后正好浇完,也就是说遍历每一个速度,求浇完花园的最少时间,没有就输出-1。
#include<bits/stdc++.h>
using namespace std;
using ll = long long;
const int N = 1e5 + 9;
#define int long long
const int MOD = 998244353;
int qmi(int a, int b, int p) {
int res = 1;
while (b) {
if (b & 1) res = res * a % p;
a = a * a % p;
b >>= 1;
}
return res;
}
int inv(int x) {return qmi(x, MOD - 2, MOD);}
int gcd(int a, int b) {return b > 0 ? gcd(b, a % b) : a;}
int lcm(int a, int b) {return a / gcd(a, b) * b;}
int n, k, a[N];
void solve() {
cin >> n >> k;
for (int i = 1; i <= n; ++ i) cin >> a[i];
int ans = 1e9;
for (int i = 1; i <= n; ++ i) {
if (k % a[i] == 0) ans = min(k / a[i], ans);
}
if (ans == 1e9) cout << -1 << "\n";
else cout << ans << "\n";
}
signed main() {
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
int _ = 1;
//cin >> _;
while (_--) solve();
return 0;
}B. 勇闯高塔
题目描述
很久很久以前,宇宙混沌一片,一天,一位神祇出现,凭借一把巨大的神斧将混沌撕裂,混沌渐渐分开,形成了天和地。在那之后,神祇并没有把祂的开天斧带走,那只巨斧被留在了地面上,化形成了一座高塔。
传说中,在高塔的顶端,遗留着开天神的宝藏,关于宝藏,有的人说是无数的金银珠宝,有的人说是绝世神斧,众说纷纭,但是宝藏的真面目,没人看到过,也没人知道。但是人们清楚的是,在高塔内,有长期待在里面的生物吸收了开天斧留下的灵气,作为了守护神守卫着高塔的宝藏。
这天,有一位勇者为了看清宝藏的真面目,闯进了高塔内,𝑛个血量为𝑎的怪物出现在了勇者面前。
勇者有两个技能:
血量交换:选择𝑖、𝑗、𝑏,交换𝑎𝑖 和𝑎𝑗的二进制表示中的第𝑏b个数字。
斩击:发出一次斩击。造成一次值为max(𝑎)−min(𝑎)的伤害。
勇者希望节省力气,尽量少的发动斩击,而血量交换因为不消耗体力,可以执行任意次。
求发动一次斩击能达到的最大伤害量。
在二进制表示中,位从右(最低有效)到左(最高有效)编号。考虑到任何二进制表示形式的开头都有无限数量的前导零位。
例如,将4=(100)2 和3=(11)2的第0位交换将得到(101)2=5和(10)2=2。将4=(100)2和3=(11)2的第2位交换将得到(000)2=0和(111)2=7。
其中,max(𝑎)表示数组𝑎的最大元素,min(𝑎)表示数组𝑎的最小元素。
𝑥的二进制表示是用基数2编写的𝑥。例如,以2为基数编写的9和6分别为1001和110。
输入描述
第一行包含一个整数 𝑡 ( 1 ≤ 𝑡 ≤ 128 ) — 测试用例的数量。
每个测试用例的第一行包含一个整数 𝑛 ( 3 ≤ 𝑛 ≤ 512 ) — 数组 𝑎 的长度。
每个测试用例的第二行包含 𝑛 个整数 𝑎1 , 𝑎2 , … , 𝑎𝑛 ( 0 ≤ 𝑎𝑖 < 1024 ) — 数组 𝑎 的元素。
确保所有测试用例的 𝑛 之和不超过 512 。
输出描述
对于每个测试用例,打印一个整数 max(𝑎)−min(𝑎) 的最大可能值。
输入样例1
4
3
1 0 1
4
5 5 5 5
5
1 2 3 4 5
7
20 85 100 41 76 49 36输出样例1
1
0
7
125思路
赛时只要5个人做出来了B题,我觉得思路蛮简单的,可能都差在实现上了。
其实就是从二进制的每一位中去看数组中所有的数的情况,是1和0都有,还是只有0或只有1,这一位只要有1,那么mx值就要加上这一位的二次幂,如果没有0,那么mn也要加上这一位的二次幂,最后求出结果即可。
#include<bits/stdc++.h>
using namespace std;
using ll = long long;
const int N = 1e5 + 9;
#define int long long
const int MOD = 998244353;
int qmi(int a, int b, int p) {
int res = 1;
while (b) {
if (b & 1) res = res * a % p;
a = a * a % p;
b >>= 1;
}
return res;
}
int inv(int x) {return qmi(x, MOD - 2, MOD);}
int gcd(int a, int b) {return b > 0 ? gcd(b, a % b) : a;}
int lcm(int a, int b) {return a / gcd(a, b) * b;}
int n, a[N];
int cnt0[N], cnt1[N];
void solve() {
cin >> n ;
for (int i = 1; i <= n; ++ i) cin >> a[i];
memset(cnt0, 0, sizeof cnt0);
memset(cnt1, 0, sizeof cnt1);
for (int i = 0; i <= 15; ++ i) {
for (int j = 1; j <= n; ++ j) {
int u = a[j] >> i & 1;
u ? cnt1[i] ++ : cnt0[i] ++;
}
}
int mx = 0, mn = 0;
for (int i = 0; i <= 15; ++ i) {
if (cnt1[i]) mx += qmi(2, i, MOD);
if (cnt0[i] == 0) mn += qmi(2, i, MOD);
}
cout << mx - mn << "\n";
}
signed main() {
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
int _ = 1;
cin >> _;
while (_--) solve();
return 0;
}C. A+B
题目描述
Joker手里有两个正整数𝑎,𝑏a,b,他发现𝑎 ⊕𝑏=\frac{a+b}{2}(𝑎+𝑏一定为偶数),Joker有些笨笨的,他只能记住一个数字,所以他只记住了𝑎⊕𝑏,我们把这个数字记为𝑥。
请帮他找到合适的𝑎和𝑏,或者告诉他这两个数字不存在
输入格式
第一个整数 𝑇(1 ≤ 𝑇 ≤ 104) 表示样例个数
对于每一个样例:
给出一个整数 𝑥(1 ≤ 𝑥 ≤ 229) ,表示Joker记住的数字
输出格式
对于每组测试样例,输出𝑎,𝑏(0<𝑏<𝑎≤232) ,如果有多个答案,则输出其中𝑎最大的一组,如果没有匹配的答案,则输出−1
输入样例1
5
6
18
10
7
36输出样例1
-1
27 9
15 5
-1
54 18思路
这道题我是根据一个结论做出来的,a \oplus b = |a - b|,事实上好像没有最大最小之分,应该是只有这一个结果。
因为a大于b,所以我们可以直接去绝对值,又a \oplus b = x, a + b=2x,可以推出a=\frac{3}{2}x,b=\frac{1}{2}x,再去异或一下,看看结果是否为x即可。
#include<bits/stdc++.h>
using namespace std;
using ll = long long;
const int N = 1e5 + 9;
#define int long long
const int MOD = 998244353;
int qmi(int a, int b, int p) {
int res = 1;
while (b) {
if (b & 1) res = res * a % p;
a = a * a % p;
b >>= 1;
}
return res;
}
int inv(int x) {return qmi(x, MOD - 2, MOD);}
int gcd(int a, int b) {return b > 0 ? gcd(b, a % b) : a;}
int lcm(int a, int b) {return a / gcd(a, b) * b;}
int x;
void solve() {
cin >> x;
if (x & 1) {
cout << -1 << "\n";
return;
}
int a = x / 2 * 3, b = x / 2;
if ((a ^ b) == x) cout << a << " " << b << "\n";
else cout << -1 << "\n";
}
signed main() {
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
int _ = 1;
cin >> _;
while (_--) solve();
return 0;
}D. 到底有几个呢?
题目描述
给出由 𝑛 个整数构成的数组 𝑎,计算数组中 1 ≤ 𝑙 ≤ 𝑟 ≤ 𝑛 的子数组的数量,使得数组 𝑏=[𝑎𝑙,𝑎𝑙+1....𝑎𝑟] 在数组𝑎中作为子序列(可以不连续)只出现了一次。
输入格式
第一个整数 𝑇(1 ≤ 𝑇 ≤ 104) 表示样例个数。
对于每一个样例:
第一行给出一个整数 𝑛 (1 ≤ 𝑛 ≤ 105) 数组𝑎 的大小。
第二行包括𝑛个整数𝑎1 , 𝑎2 ..... 𝑎𝑛(1 ≤ 𝑎𝑖 ≤ 109)
保证所有测试样例中的𝑛n的总和不超过2×105。
输出格式
对于每组测试样例,输出满足条件的子数组的数量
输入样例1
6
1
1
2
3 3
3
11 25 11
4
4 3 4 1
5
4 5 4 5 4
10
1 71 71 22 3 42 3 22 1 100输出样例1
1
1
4
7
4
28思路
当时没想到一些关键点,所以一直没做出来,由于要用到子数组要作为子序列去看有没有相同的,其实相当于把你的子数组的端点向两边扩散看看有没有和端点一样的

像这样的就是从左端点向左找1,从右端点向右找9,只要都没有找到,这个子数组就是合格的。
我们可以把每一个数第一次出现的下标存入一个 vector,然后就从后往前找,只要找的数是第一次从后面出现,即是数组中最后一次出现,那么这个数就可以作为我们的右端点。
然后我们再从 vector 中寻找我们的右端点,在这下标之前的只要是第一次出现的都可以作为左端点,所以可以在下标数组中用 upper_bound 二分去查找第一个大于右端点的下标,往前的都是符合条件的左端点,因此答案直接加上下标值即可。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 1e5 + 10;
int a[N];
map<int , int>cnt , ind , vis;
int main()
{
ios::sync_with_stdio(0) , cin.tie(0) , cout.tie(0);
int _;cin >> _;
while(_--)
{
cnt.clear(); ind.clear();vis.clear();
int n;cin >> n;
ll ans = 0;
vector<int>l , r;
for(int i = 1;i <= n;i++)
{
cin >> a[i];
if(cnt[a[i]] == 0) l.push_back(i) , r.push_back(a[i]);
cnt[a[i]]++;
ind[a[i]] = i;
}
for(int i = n;i >= 1;i--)
{
if(!vis[a[i]])
{
int p = upper_bound(begin(l) , end(l) , ind[a[i]]) - begin(l);
ans += p;
vis[a[i]] = 1;
}
}
cout << ans << '\n';
}
return 0;
}E. 小e要种树
题目描述
作为一个优秀的大学生,当然要心系社会啦!这一天小 𝑒 同学心血来潮准备去做一些有益于社会的事情,小 𝑒 思来想去决定出发去种树!
在小 𝑒 到达种树的地方之后,发现一共有𝑛棵树。它们的高度依次为𝑎𝑖米。
小 𝑒 突发奇想,如果选出一些树,让它们保持原来的相对顺序,并且从左至右构成了一个公差不小于零的等差数列,那么这个顺序就会被认为是美观的。
小 𝑒 想知道,到底有多少种顺序是美观的呢?请你帮他解决这个问题。
输入描述
第一行一个整数 𝑛 ( 1 ≤ 𝑛 ≤ 103)
第二行 𝑛 个非负整数,第 𝑖 个数是第 𝑖 棵树的高度𝑎𝑖 ( 1 ≤ 𝑛 ≤ 2∗104)
输出描述
输出一个整数,表示美观的顺序种类取模 903261123 后的值。
输入样例
6
13 6 27 34 34 41输出样例
23思路
读完题很容易联想到dp,其实是求上升子序列的数量,但是我不会qwq。
看了题解的 dp 做法,好像简单了一些,不过这个模数好阴间。
dp[i][a[i]−a[j]]=(dp[i][a[i]−a[j]]+(dp[j][a[i]−a[j]]+1))\% mod
#include<bits/stdc++.h>
using namespace std;
using ll = long long;
const int N = 1e3 + 9;
#define int long long
const int MOD = 903261123;
int qmi(int a, int b, int p) {
int res = 1;
while (b) {
if (b & 1) res = res * a % p;
a = a * a % p;
b >>= 1;
}
return res;
}
int inv(int x) {return qmi(x, MOD - 2, MOD);}
int gcd(int a, int b) {return b > 0 ? gcd(b, a % b) : a;}
int lcm(int a, int b) {return a / gcd(a, b) * b;}
int n, dp[N][20000 + 9];
int a[N];
void solve() {
cin >> n;
for (int i = 1; i <= n; ++ i) cin >> a[i];
int ans = 0;
for (int i = 1; i <= n; ++ i) {
ans ++;//自己也算一个序列
for (int j = 1; j < i; ++ j) {
if (a[i] >= a[j]) {
dp[i][a[i] - a[j]] = (dp[i][a[i] - a[j]] + dp[j][a[i] - a[j]] + 1) % MOD;
ans = (ans + dp[j][a[i] - a[j]] + 1) % MOD;//每次都会加上一点,我们只拿每次加的一点结果仍为总和
}
}
}
cout << ans << "\n";
}
signed main() {
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
int _ = 1;
//cin >> _;
while (_--) solve();
return 0;
}
